
The purpose of this chapter is to explain the physical phenomena carefully and to fully understand the interaction of high energy X-rays and matter about the principle and the knowledge of basic physics needed for a SBRT. As a result, in the SBRT, the dose deposit and the dose distribution differ in a homogeneous and heterogeneous domain in the patient body. Therefore, the energy of the recoil electron is dependent on the kind of interaction, and the kinetic energy of the incident photon. The reaction cross section of the photoelectric effect, Compton scattering, and pair production depends on the energy of the photons. In these interactions, this energy is transferred from photons to electrons. The kinetic energy of X-rays is given for the delivery dose of a tumor by physical interactions of photons with matter, and so the photoelectric effect, Compton scattering, and pair production are important interactions for a SBRT. Other experimental observations are cited which also lead to the conclusion that the first postulate is much more likely to be true than the second, hence, that each quantum of scattered radiation is probably emitted in a definite direction.In stereotactic body radiation therapy (SBRT) for the lungs and the liver, high-energy X-rays provided from a linear accelerator (Linac) are irradiated to a tumor with the high dose of about 10 Gy. The formula presumes that the scattering occurs in the rest frame of the electron. The second postulate, however, leads to a value for E m only one-fourth that given above, a value which is inconsistent with that derived from a consideration of radiation pressure and which leads to values for maximum ranges one-fiftieth of those observed by Wilson. and is called the Compton wavelength for the electron. The relative number of recoil electrons to photo-electrons increases with the frequency and is in agreement with observations by Wilson.
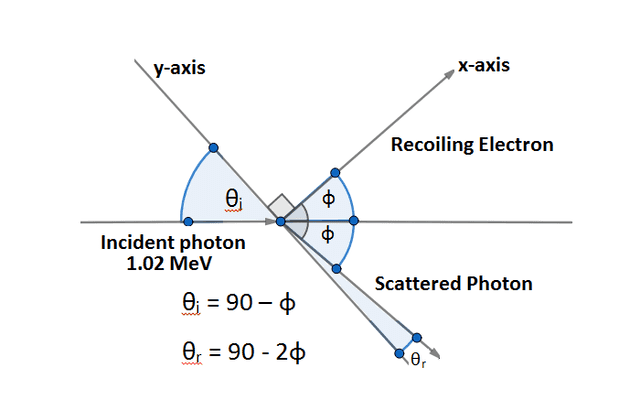
The values for the maximum ranges in the case of x-rays (.34 to.48 A) are computed to be about one-third of those observed by Wilson for his fish tracts, but the difference may be due to the lack of homogeneity of the rays used. The maximum range increases rapidly with frequency. Wilson, the distribution of ranges is found to be such that two-thirds have tracks shorter than half the maximum range. 15- angle at which the recoil electron is ejected has been. where Pe is the momentum of the electron after scattering. I wrote down the equations of conservation of linear momentum in x and y directions.
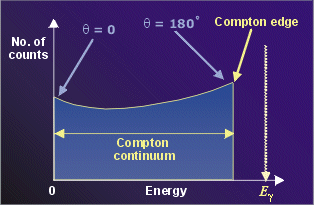
the relation: Where f is the frequency of incident photon. On the first postulate the maximum recoil energy is shown to be E m = h ν 0 × 2 α ( 1 + 2 α ), where α = h mc λ 0 the recoil electrons are shown to be concentrated at angles near the direction of the primary beam and from the distribution of energy, using a relation given by C. The relation between the engle of scattering and the. Show that the scatter angles of the photon () and electron () in the Compton effect are related by. Expressions for the distribution of recoil velocities, of energies and of ranges are developed for each of two postulates, assuming (1) the scattered radiation consists of directed quanta, and (2) the scattered radiation proceeds as spherical waves. Figure 2: 300 MeV protons (CSDA and energy straggling) and. Since this is a two body elastic scattering process, the angle of the scat-tered photon is completely correlated with the energy of the scattered photon by energy and momentum conservation. Quantum theory of the recoil of electrons from scattered x-rays.-This is an extension of the quantum theory of scattering suggested by Compton, which assumes that each directed x-ray quantum is scattered by a single electron. Energy of the recoil photons by Compton scatter-angle distribution of forward and lateral scatter. The Compton eect is the elastic scattering of photons from electrons.


 0 kommentar(er)
0 kommentar(er)
